Математична основа класифікації KNN в економіці
Анотація: У даній роботі розглянуто метод k найближчих сусідів (K-Nearest Neighbors, KNN) — один з базових алгоритмів машинного навчання, що використовується для задач класифікації та регресії. Основна ідея алгоритму полягає у визначенні класу або значення нового об’єкта на основі більшості або середнього значення його найближчих сусідів у навчальній вибірці. Метод не потребує етапу навчання, що робить його простим у реалізації, але ресурсоємним при обробці великих обсягів даних. У роботі проаналізовано принцип роботи KNN, критерії вибору параметра k, метрики відстані, переваги, недоліки та можливості оптимізації. Також наведено приклади практичного застосування алгоритму у задачах розпізнавання образів, медичних діагнозах та рекомендаційних системах.
Вступ. У повсякденному житті часто потрібно віднести об’єкт до певної категорії за його ознаками - це класифікація. Прикладом в економіці є сегментація ринку, тобто розподіл споживачів за інтересами, віком чи доходом для точнішого націлення реклами та послуг.
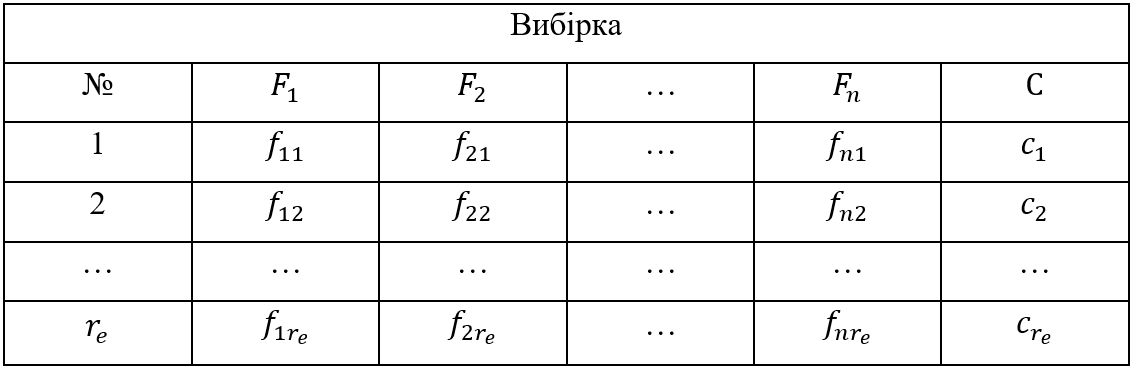
Постановка задачі. Дана вибірка з генеральної сукупності оформлена у вигляді таблиці, що містить r_eточок даних (записів) (див. табл. 1). Кожна точка даних складається з n значень f ознак F_i (feature) та мітки с класу С (class) до якого вона належить. На вхід поступає нова точка даних з певними значеннями ознак (f_i )_(i=1)^n, визначити найбільш ймовірну мітку.
Векторизація. Для того щоб алгоритми штучного інтелекту могли працювати з даними різного типу уніфіковано (незважаючи на природу цих даних) необхідно розробити єдиний формат подання даних. Одним з таких форматів є вектор чисел. Кожна координата такого вектора містить відцифроване представлення значення відповідної ознаки. Процес представлення початкових даних у вигляді числового вектора - векторизація.
Дискримінантний аналіз. Розділ математики, який вивчає методи дискримінації (класифікації) об’єктів на основі їхніх ознак. Ціль дискримінантного аналізу: на основі ознак об’єктів провести їх дискримінацію, тобто віднести їх до одного з відомих класів. Робиться припущення, що об’єкти одного класу мають схожі ознаки [1]. Дискримінантна функція g_c (x) - функція за допомогою якої на основі ознак оцінюють схожість об’єкта на об’єкти класу c. Об’єкту присвоюється мітка класу з найбільшою оцінкою дискримінантної функції (найбільшою схожістю), тобто:
\[ y ̂_x=argmax_x g_c (x) \]
Постає питання: яким чином можна чисельно оцінити схожість двох об’єктів? Відповідь - за допомогою задання метричного простору. Метричний простір - пара (M,d), де M - множина, d:M×M→R - функція відстані.
d(x,y)=0⇔x=y (аксіома тотожності) d(x,y)≥0 (аксіома невід’ємності) d(x,y)=d(y,x) (аксіома симетричності) d(x,y)≤d(x,y)+d(y,z) (аксіома трикутника)
Аксіоми 1, 2, 3 інтуїтивно відповідають людському уявлення про відстань, аксіома 4 потребує додаткових пояснень. Вона постулює, що відстань є найкоротший шлях з усіх можливих. Візьмемо 3 точки: A,Б, та В (елементи множини M). Розглянемо наступні 3 шляхи:
d(A,Б) (прямий шлях) d(A,В) (частина 1 транзитного шляху через В) d(В,Б) (частина 2 транзитного шляху через В)
Очевидно, що існує 2 варіанти як дістатися від A до Б: прямий шлях та транзитний шлях. Людське уявлення про відстань каже нам, що найкоротший варіант - прямий. В той же час, якщо транзитна точка (В) лежить на прямому шляху, то прямий шлях по довжині дорівнює транзитному. Якщо ж транзитна точка не лежить на прямому шляху, то довжина транзитного шляху буде більшою за прямий. Саме це людське уявлення і описує 4-а аксіома. Приклади поширених функцій відстані. Евклідова відстань.
\[ d(x,y)=||x-y||=(∑_(i=1)^n(x_i-y_i )^2 )^(1/2) \]
Косинус подібності.
\[ d(x,y)=cos(<(x,y))=xy/(|x||y|) \]
Нормалізація. На практиці часто доводиться мати справу з двома і більше ознаками. Ці ознаки можуть мати різні діапазони можливих значень. Це в свою чергу може призвести до проблеми, коли одна ознака має значно менший діапазон можливих значень ніж інша, і через це при підрахунку відстані ознака з меншим діапазоном майже не враховується, хоча вона може бути важливою ознакою для дискримінації. Для усунення цієї проблеми використовується нормалізація - приведення усіх ознак до одного діапазону можливихи значень. Таким чином, кожна ознака враховується незалежно від свого діапазону можливих значень [2].
Приклади поширених нормалізацій. Мінімаксна-нормалізація.
\[ f'=(f-min[F])/(max[F] - min[F]) \]
Z-нормалізація.
\[ f'=(f-M[F])/(σ[F]) \]
KNN з незваженим голосуванням. На вхід подається вектор x. Обирається k найближчих до x векторів - сусідів . Вектору z присвоюється мітка класу більшості сусідів, тобто:
\[ g_c (x)=∑_(x_c∈ c) I_c (x) \]
I_c (x)-індикаторна функція,I_c (x)=1⇔x∈C;I_c (x)=0⇔x∉C
Такий підхід має суттєвий недолік: він робить припущення, що всі сусіди мають однакову вагу голосу, незалежно від того наскільки близько вони розміщенні до x. Проблему дозволяє вирішити введення вагової фнкції.
Вагова функція w:A→R^+ - функція, яка використовується для того, щоб при сумі або інтегровані зробити внесок елементів множини A в результат неоднаковим. Прикладом є обернена відстань.
Обернена відстань.
\[ w(x,y)=1/(d(x,y)+ε) \]
ε - мала додатня константа, що дозволяє уникнути ділення на 0 коли d(x,y)=0.
KNN із зваженим голосуванням. На вхід подається вектор x. Обирається k найближчих до x векторів - сусідів. Обраховується внесок кожного з сусідів. x присвоюється мітка сусідів одного класу, зробивших найбільший внесок.
\[ g_c (x)=∑_(x_c∈ c) I_c (x)w(x,x_c) \]
Висновок. Таким чином, представлено метод KNN як один із варіантів розв’язання задачі класифікації. Питання визначення оптимального значення параметра k залишилось відкритим.
Література
- GeeksforGeeks. K Nearest Neighbors (KNN) Algorithm. URL: https://www.geeksforgeeks.org/ml-k-nearest-neighbors-algorithm/ (дата звернення: 28.02.2025).
- Scikit-learn. Nearest Neighbors. URL: https://scikit-learn.org/stable/modules/neighbors.html (дата звернення: 28.02.2025).